拉普拉斯变换
傅里叶变换推广为拉普拉斯变换
- 基底信号从
推广成 - 其中
为复平面上的值 - 当
为纯虚数 拉普拉斯变换退化为傅里叶变换
- 其中
- 拉普拉斯变换定义
- 定义初衷
时不满足绝对可积条件,此时原信号不存在傅里叶变换
- 正变换
- 把
乘以衰减因子 再傅里叶变换(令 )
- 把
- 逆变换
- 对
做逆傅里叶变换, - 故
- 可以看出逆变换的积分路径是复平面的一条直线
- 对
- 定义初衷
- 符号表示
- 物理意义
- 信号可以分解成
的线性组合 是复频率, 是复频谱
- 信号可以分解成
单边拉普拉斯变换
对于因果系统,单边拉普拉斯变换更方便,本节后续主要考虑单边的拉普拉斯变换
拉普拉斯变换的收敛域
- 使拉普拉斯变换积分收敛的那些复数
的集合,称为拉普拉斯变换的收敛域ROC - 如果拉普拉斯变换的ROC包含
轴,则有
- 如果拉普拉斯变换的ROC包含
- 零极点图
- 若
- M是常数,分子多项式的根是零点,分母多项式的根是极点
的全部零点和极点在 平面上构成了零极点图 - 零极点图和收敛域可以表示一个
,与真实的 最多差一个常数因子
- 零极点图和收敛域可以表示一个
- ROC总是以平行于
轴的直线为边界,该边界对应一个极点
- 若
常见信号的拉普拉斯变换
- 指数型函数
- 同理
- 三角函数
- 阶跃函数
- 冲激信号
的正幂函数 ,其中 是正整数 - 根据以上可递推
- 根据以上可递推
拉普拉斯变换的性质
- 线性
- 若
- 且
- 则
- 若
- 时移性质
- 若
- 则
- 若
- S域平移
- 若
- 则
(即ROC发生平移)
- 若
- 时域尺度变换
- 若
- 则
(即ROC边界乘以 )
- 若
- 共轭对称性
- 若
- 则
- 若
- 时域卷积性质
- 若
- 则
- 若
- 时域微分
- 若
- 则
- 对于双边拉普拉斯变换,
,ROC包括 ,有可能扩大 - 对于单边拉普拉斯变换,
,ROC包括 ,有可能扩大
- 若
- S域微分
- 若
- 则
- 若
- 时域积分
- 若
- 则
- 对双边拉普拉斯变换有
- 对单边拉普拉斯变换有
- 对双边拉普拉斯变换有
- 若
- 初值定理
- 若
是因果信号,在 处不存在奇异函数
- 则
- 证明思路是将
在 处展开为泰勒级数,然后进行拉普拉斯变换得
- 若
- 终值定理
- 若
是因果信号,在 处不存在奇异函数, 的收敛域含
- 则
- 证明思路是用拉普拉斯变换的时域微分性质,取极限
- 若
拉普拉斯反变换求解
- 定义法
- 留数定理
- 在特定条件下能把线积分转化为环路积分
- Jordan引理:当
满足在左半平面 内只有有限个奇点,且 时 ,则 - 在Jordan引理条件下
- Jordan引理:当
- 再根据留数定理得
为函数 在封闭曲线 内的所有孤立奇点 - 这里只考虑
是连续函数
- 在特定条件下能把线积分转化为环路积分
- 部分分式展开法
- 思路
- 根据拉普拉斯变换的线性特性,把复杂的拉普拉斯变换展开为多个简单拉普拉斯变换的组合,并对这些简单变换求反变换,从而求解原拉普拉斯反变换
- 步骤
- 找出
的极点 - 将
展开成部分分式 - 由部分分式直接写出时域表达式
- 找出
- 具体细节可以搜索查公式表,此处从略
- 思路
连续时间系统的复频域分析
连续时间系统的系统函数
- 原理和定义
- 复指数函数是一切LTI系统的特征函数
- 以
为基底分解信号,输入信号的输出响应是 , 是系统的频率响应 - 以
为基底分解信号,输入信号的输出响应是 , 即 的拉氏变换,称为系统函数或传输函数
- 以
- 复指数函数是一切LTI系统的特征函数
- 求解方法
- 系统在零状态条件下,输出信号的拉氏变换和输入信号的拉氏变换的比值
- 对冲激信号的响应
进行拉氏变换得到
- 系统在零状态条件下,输出信号的拉氏变换和输入信号的拉氏变换的比值
- 求解零状态响应
- 时域卷积
域乘积
- 时域卷积
系统函数与系统特性
- 系统时域特性
,指数衰减; ,指数增加
,等幅振荡 ,衰减振荡 ,增幅振荡
- 系统的因果性
- 有物理意义的物理系统都是因果系统
时
是有理函数的系统为因果系统的充要条件 的收敛域是 域的某个右半平面
- 有物理意义的物理系统都是因果系统
- 系统的稳定性
- 连续时间线性时不变系统稳定的充要条件
- 因果系统在
域稳定的充要条件 - 系统函数
全部极点在 平面的左半平面(极点实部小于零)
- 系统函数
- 连续时间线性时不变系统稳定的充要条件
- 系统的频响特性
- 含义
- 正弦信号激励下,系统稳态响应随信号频率变化特性
- 分析
- 令系统响应取
,即 和 分别称为幅频响应和相频响应
- 令系统响应取
- 含义
微分方程描述系统的复频域分析
- 求解时域微分方程可以得到系统时域响应
- 求解
域代数方程可以得到系统 域响应 - 通过拉氏变化可以把系统的微分方程转化为代数方程求解
- 对输出响应
进行拉普拉斯反变换,得到
连续时间线性系统的框图描述
- 系统的基本构成单元
- 加法器
- 标量乘法器
- 积分器
- 系统的基本联接
- 定义
- 多个系统的组合连接构成复杂系统,称为复合系统
- 组成复合系统的每个系统称为子系统
- 组合连接方式
- 串联:

- 并联:
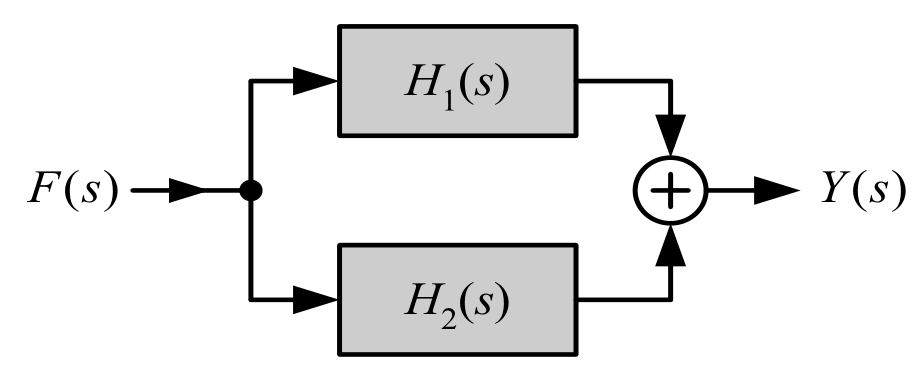
- 反馈环路:
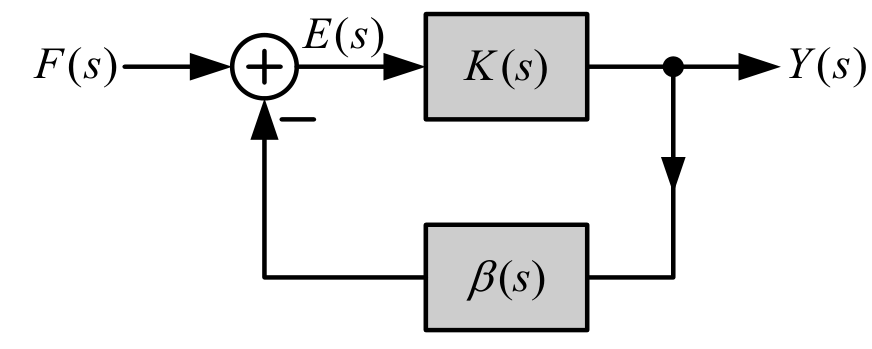
- 串联:
- 定义
