【知识总结】z变换与离散时间系统的z域分析

z变换与反变换

z变换定义

• 双边z变换
• 单边z变换
  • • 是复变量，上同
    • 对于因果信号，单边z变换和双边z变换相等，否则不等

z变换与傅里叶变换

• 令
  • • 当，序列z变换就是傅里叶变换

z变换与拉普拉斯变换

• 从抽样信号的拉氏变换可以推导出z变换
  • 设是连续因果信号
    • 则冲激抽样得到
  • 对抽样信号进行单边拉氏变换
    • 最后一步推导用到冲激函数的取样特性
  • 令，则
    • 得到z变换

z变换的收敛域

• z变换收敛要求
  • 收敛条件的要求低于傅里叶变换的收敛条件
    • 满足上式的z值构成的集合是的收敛域ROC
• 的收敛域是在z平面内以原点为中心的圆环
  • 收敛域形式一般为
• z变换收敛域内不包含极点
  • 因为在极点处值无穷大，z变换不收敛
  • 通常以极点作为收敛域的边界

基本离散信号的z变换

• 单位脉冲序列
• 单位阶跃序列
• 斜变序列
  • • 计算时可以在两边对求导
• 单边指数序列
  • • 非因果序列有
• 双边指数序列
  • • 观察收敛域，可知时z变换才存在
• 正余弦序列

z变换基本性质

• 线性性质
  • 若
  • 则
    • 若线性组合中某些零点的引入抵消了部分极点，收敛域可能变大
• 位移性质（双边z变换）
  • • 证明：
    • 在和无穷处零极点情况发生变化
• 位移性质（单边z变换）
  • • 证明：
    • 在和无穷处零极点情况发生变化
• 频移性质
• 序列指数加权
• 时间反转
  • • 证明：
    • 若在的z变换收敛域内，则在的z变换收敛域内
• z域微分
  • • 证明：
• 卷积定理
  • • 证明：
    • 通常收敛域是和收敛域的交集，若位于某一z变换收敛域边界上的极点被另一z变换的零点抵消，则收敛域可能扩大
• 共轭性质
  • 若
  • 则

z反变换

• 定义
• 求解方法
  • 查表法
    
  • 留数法
    • 一种计算封闭曲线积分的方法，可参考复变函数内容，此处不展开讨论
  • 幂级数展开法
    • 当能表示为幂级数的形式，则
  • 部分分式展开法
    • 当序列是分数形式，将其展开为典型分数序列的线性组合，再查表求解

离散系统的z域分析

用z变换求解差分方程

• 原理
  • 设阶离散系统差分方程为
  • 把差分方程转换为代数方程，在域求出系统函数
• 零状态响应推导
  • 上述差分方程两侧单边z变换并利用时域性质得
  • 考虑系统处于零状态，即时
  • 当是因果序列，即时
  • 此时离散系统的系统函数为
  • 从而差分方程转化为代数方程
    • 系统零状态响应是
• 零输入响应推导
  • 系统处于零输入，即，此时差分方程变为齐次方程
  • 单边z变换得
  • 从而差分方程转化为代数方程
    • 零输入响应是

系统函数零极点分布与系统特性

• 设
  • 是零点，是极点
  • 则
  • 当收敛域有
    • 说明的极点决定的特性，零点只影响的幅度和相位
• 因果特性
  • 极点位于单位圆内，收敛域为
    • 的幅度随衰减
  • 极点位于单位圆外，收敛域不包括单位圆
    • 的幅度随递增
  • 极点在单位圆上
    • 为等幅或正负交替的等幅形状
• 稳定特性
  • 系统稳定充要条件是
    • z变换收敛域定义
  • 系统稳定的相关结论
    • 当在处收敛，系统稳定
    • 对于因果系统，若收敛域，则绝对可和，从而系统稳定

系统函数的零极点求频率响应

• 设系统函数为
• 当收敛域包含的单位圆，将带入上式即可得到频率响应

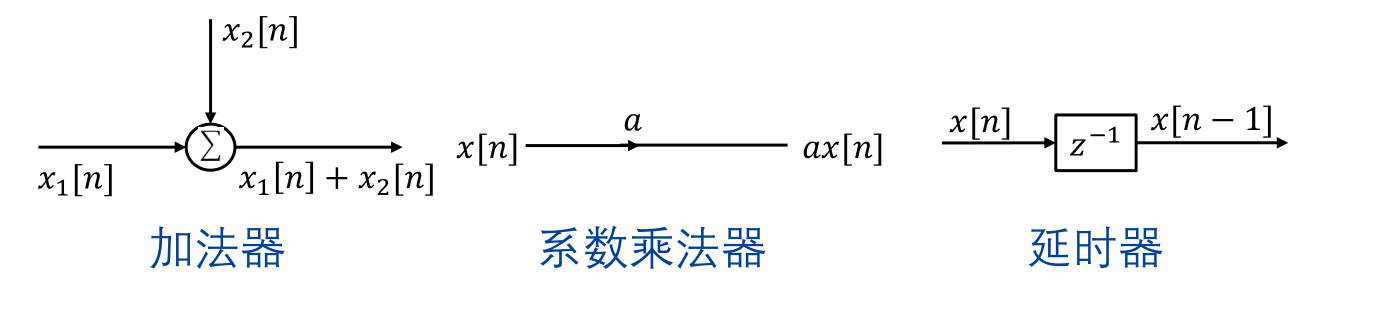
离散时间系统的框图描述