0%

【知识总结】信号的频域分析

发表于 2022-09-05 更新于 2023-09-25 分类于信号与系统阅读次数：评论数：

连续时间信号的频域分析

引言

信号分解的基本单元一般满足
- 用基本单元进行线性组合可以简单表示原信号
- 基本单元的响应容易求得
信号时域分解的基本单元冲激函数就满足上述条件
信号频域分解的基本单元是
- 这里给出该基本单元的响应
  - 即，该基本信号只产生了系数的变化
- 后面的内容会介绍如何把原信号频域分解成基本单元

傅里叶级数

本节介绍狭义的傅里叶级数，默认用在连续周期的时域信号

周期信号的傅里叶级数展开

展开条件（Dirichlet条件）
- 在任何周期内绝对可积，即
- 在一个周期内只有有限个有限的不连续点，且这些不连续点的值有限
- 在一个周期内只有有限个极大值和极小值
指数形式傅里叶级数
- - 其中，称为傅里叶级数系数或频谱系数，通常是复数（所以有时叫复振幅）
  - 是基波角频率，是基波频率
- 各项解释
  - ：直流分量
  - 两项：基波频率为，合起来为信号基波分量
  - 两项：基波频率为，合起来为信号次谐波分量
  - 两项：基波频率为，合起来为信号次谐波分量
三角形式傅里叶级数
- 考虑是实函数的情况，
  - 则
- 因此
  - 即
- 又，令，则有
- 纯余弦形式傅里叶级数
  - 是信号的直流分量
  - 是信号的次谐波

周期信号的频谱及其特点

频谱的概念
- 频谱的函数，称为频率函数
  - 反应组成信号各正弦谐波的幅度合相位随频率变化的规律
频谱的表示
- - 是幅度频谱函数
  - 是相位频谱函数
- 画出频谱函数对应的线状分布图形，即频谱图
- 信号的基频和频谱可以确定一个信号
频谱的特性
- 离散性
  - 谱线间隔
  - 信号周期越大，谱线越密集
- 衰减性
  - 随着增大，衰减并趋近于零
  - 信号时域波形变化越平缓，高次谐波越少，幅度频谱衰减越快

周期信号的功率谱

Parseval 功率守恒定理
- - 任意周期信号平均功率等于信号包含的直流、基波、各次谐波的平均功率之和
周期信号的功率频谱
- 随分布情况
  - 简称功率谱

傅里叶变换

本节从傅里叶级数引出傅里叶变换，从而无论信号是否有周期性，都可求解频谱

从傅里叶级数到傅里叶变换
- 对于非周期信号，可以认为其周期无穷大（，是傅里叶系数）
  - 则频谱满足
  - 此时任何频率值对应的频谱函数的值都是无穷小，
  - 记为频谱密度函数，一般简称频谱函数
频谱函数和频谱密度函数的区别
- 周期信号的频谱是离散的，非周期信号的频谱是连续的
- 周期信号的频谱是的分布，非周期信号的频谱是的分布
傅里叶反变换
- 写成积分形式，即考虑时，，则
狄里赫利条件（非周期信号存在傅里叶变换的充分不必要条件）
- 非周期信号在无限区间上绝对可积
- 在任意有限区间内，信号只有有限个最大值和最小值
- 在任意有限区间内，信号仅有有限个不连续点，且这些点都是有限值

常见连续时间信号的频谱密度

非周期信号

单边指数信号
双边指数信号
单位冲激信号
冲激偶信号
直流信号（不满足绝对可积条件，考虑用极限法或逆傅里叶法）
- 极限法
  - 时，否则
  - （取不影响该条件的满足）
  - 因此
- 逆傅里叶变换
符号函数信号
- 考虑到
- 则
单位阶跃信号
- 考虑
- 则

周期信号

虚指数信号
- 考虑
  - 即利用前面小节，直流信号的频谱的结论
- 则
- 同理
正弦型信号
一般周期信号
- 把信号在时域展开成傅里叶级数，然后对每一项（虚指数信号）进行变换
- 周期函数的傅里叶频谱是傅里叶级数同位置的冲激
  - 即周期信号的两种频谱表示形式（傅里叶变换、傅里叶级数）是统一的
单位冲激序列
- 先展开为傅里叶级数
  - 注意这里算出是单位冲激序列的傅里叶系数
- 则

傅里叶变换的基本性质

本节直接列出结论，按定义推导从略

线性特性
- 若且
- 则，均为常数
时域卷积特性
- 若且
- 则
共轭对称特性
- 若
- 则
  - 当是实函数，，即和共轭
时移特性
- 若
- 则
  - 信号在时域中的时移，对应频谱在频域的相移
展缩特性
- 若
- 则
  - 时域压缩，频域展宽
  - 时域展宽，频域压缩
互易对称特性
- 若
- 则
频移特性（调制定理）
- 若
- 则
时域微分特性
- 若
- 则
积分特性
- 若
- 则
频域微分特性
- 若
- 则
频域卷积特性（调制特性）
- 若
- 则
非周期信号的能量谱密度
- - 由于是实数，故
  - 帕什瓦尔能量守恒定理：
  - 能量频谱密度函数（能量频）：

抽样信号的傅里叶变换

本节分析抽样时间信号的傅里叶变换，并介绍抽样定理，为后续的离散时间信号频域分析做铺垫

时域抽样信号的傅里叶变换
- 设时域抽样信号为
  - 是抽样前的原始连续信号
  - 是抽样脉冲序列（这里只考虑理想抽样，即单位冲激序列，也有矩形脉冲序列等抽样序列），抽样周期为，抽样频率为
- 前面已经推导了单位冲激序列的傅里叶变换为
- 由频域卷积特性得
  - 即
  - 再使用了卷积的延时特性，得
  - 理想时域抽样信号在频域内具有周期性，周期为
抽样定理
- 一个频谱受限的信号，如果频谱只占据的范围，则抽样间隔不大于，才能保证信号可以用等间隔的抽样值唯一的表示（不损失信息）。
  - 因为，从而时域的抽样导致的频域的周期化不会出现重叠
- 这里的抽样定理指的是时域抽样定理，也有类似的频域抽样定理，这里略

离散时间信号的频域分析

离散时间信号的傅里叶变换（DTFT）

本节介绍离散时间信号的傅里叶变换，即序列的傅里叶变换，信号在时域是离散的，频域通常连续（除非信号在时域是周期的）

原理
- 信号的周期性对应频谱的离散性
- 信号的离散性对应频谱的周期性
离散时间信号对应周期的频谱（密度）
- IDTFT
- DTFT
  - 频谱周期是
  - 的表达式是无穷项级数，存在收敛问题
DTFT收敛的充分不必要条件
- 若（绝对可和），则的DTFT存在且一致收敛于
- 若不是绝对可和，但是（平方可和），则的DTFT存在且以均方差为零的方式收敛于

离散傅里叶级数（DFS）

本节介绍离散傅里叶级数，信号在时域和频域都是离散周期的

考虑复指数信号集
- 因为每个信号都是以为周期且只有个信号彼此独立，因此这是一个完备正交基
- 任意以为周期的序列可以写成该完备正交基的线性组合
离散傅里叶级数（DFS）
- - 是个相连的整数
- - 是的频谱
离散傅里叶级数（DFS）和离散傅里叶变换（DFT）
- 离散傅里叶级数（DFS）是离散周期时间信号的一种频谱表示方式
  - 此时信号在时域和频域都是离散的，故直接称之离散傅里叶级数DFS，区别于DTFT的称法
  - 连续周期时间信号有傅里叶级数（FS）和傅里叶变换（FT）两种统一的频谱表示形式；离散周期时间信号有离散傅里叶级数（DFS）和离散时间傅里叶变换（DTFT）两种统一的频谱表示形式
- 离散傅里叶变换（DFT）是把有限长时间序列变换到有限长频率序列，以方便计算机处理的一种应用算法
  - 大致的思想是把有限长序列作为周期性离散信号的一个周期来处理
  - 详见后面傅里叶变换总结和补充

常用信号的离散时间傅里叶变换

矩阵脉冲；
实指数序列
非因果实指数序列
双边指数序列
- 考虑
离散时间周期信号的傅里叶变换
- 把信号在时域展开成离散傅里叶级数，然后对每一项（虚指数信号）进行变换
- 即使直接使用离散时间信号的变换公式，在计算时可能还要用到傅里叶级数的公式，详见后面周期性样值序列的傅里叶变换推导
常数序列
- 考虑
指数序列
- 考虑
余弦信号
周期性样值序列
- - 上面步骤的证明如下：令，，，再证明更一般的结论，而把展成傅里叶级数有，即从而结论成立。
  - 末尾步骤利用了冲激函数性质
- 也可以考虑使用离散周期函数傅里叶变换公式
  - 先求出
  - 故

离散时间信号傅里叶变换性质

周期性
- 若
- 则
线性
时移特性
- 若
- 则
频移特性
- 若
- 则
时间反转
- 若
- 则若
共轭对称性
- 若
- 则若
  - 进一步可知若是实信号，则，即
卷积定理
- 若
- 则
相乘性质
- 如果
- 则
  - 考虑到周期都是，所以上述卷积叫周期卷积
频域微分
Parseval定理
- - 称为的能量谱密度函数

傅里叶变换总结和补充

（理论总结）四种傅里叶变换对比

周期性对应着离散性，周期化对应着抽样

傅里叶变换（FT）
- 时域非周期连续，频域非周期连续
傅里叶级数（FS）
- 时域周期连续，频域非周期离散
离散时间傅里叶变换（DTFT）
- 时域非周期离散，频域周期连续
离散傅里叶级数（DFS）
- 时域周期离散，频域周期离散

（应用补充）离散傅里叶变换（DFT）和快速傅里叶变换（FFT）

DFT是一个应用于计算机的算法
- 时域非周期离散，频域非周期离散
- 时域频域都是有限长序列
- 具体的时域频域信号对比图如下

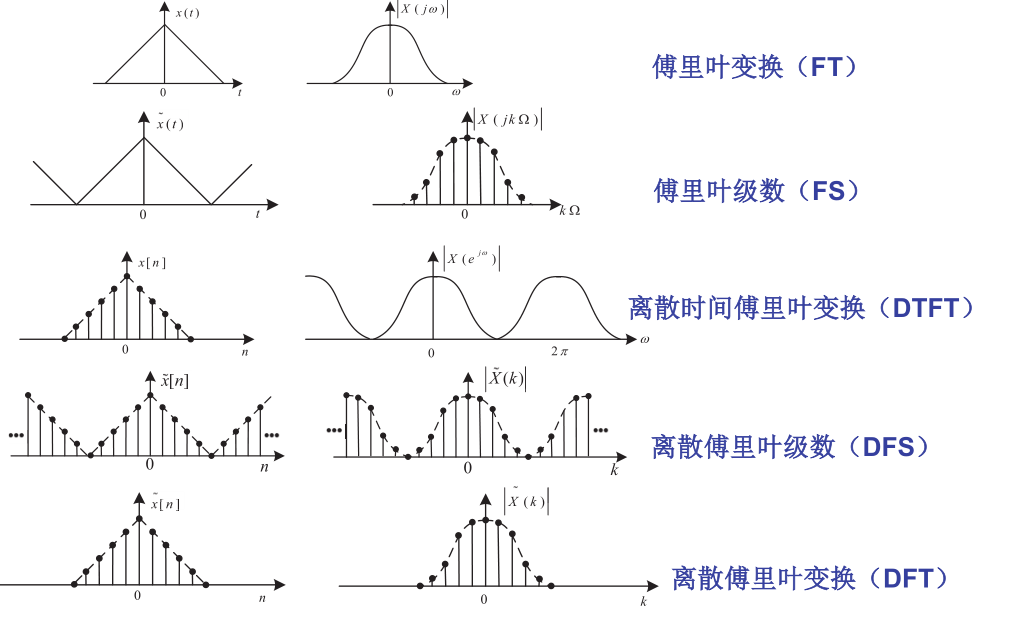
this is comparisons between five kinds of FT

FFT是一种在计算机上高效运行的具体的DFT算法
- 大概思路是把一段有限序列分成奇数下标、偶数下标两个子序列分治求解再叠加
- 用主定理分析复杂度式子为，故
- 具体参考数字信号处理的内容