【知识总结】第二章-数据的表示和运算

数制与编码

进位计数制和数据间转换

计算机内部用二进制编码信息的原因

成本方面：二进制两种状态，用有两个稳定状态的物理器件表示，制造成本低。
功能方面：二进制的两种状态，对应逻辑值“真”和“假”，方便计算机实现逻辑运算、进行逻辑判断
实现方面：二进制编码和运算简单，通过逻辑门电路很容易实现

进位计数值

常用的有十进制、二进制、八进制、十六进制等
基数：进位计数法中每个数位用到的数码个数，每满基数则向高位进位
r进制数()可以表示为，其中是数码，是基数，是位权
十六进制的基数16，每一位可以取0-9，A-F（代表10-15）中的任意一个，4位二进制数码对应1位十六进制数码

不同进制数的互相转换

二进制数转八进制（十六进制）：从小数点起，分别向左向右，每3位（4位）一组，高位或低位不足可补0
八进制（十六进制）转二进制数：每位展开成3位（4位）二进制串即可，展开后必要时去掉高位和低位的0
任意进制转十进制：各个位数码和该位权值的乘积和，即按权展开法
十进制转任意进制数：对整数部分除基数取余（相当于对应进制的整数右移溢出最后一位）；对小数部分乘以基数取整（相当于对应进制的小数左移，溢出第一位）
不是每个十进制小数都能转换成准确的二进制；每个二进制小数都可以转换成准确的十进制

定点数的编码表示

从下面数的划分中清晰的展现了知识脉络

真值：用户使用的进位计数值编码的各种进制数
机器数：计算机内部使用的数值数据，根据小数点位置是否固定分为
- 定点数
  - 无符号：直接用真值的二进制形式表示的数
  - 有符号
    - 通常用二进制最高位作为符号位，放在数字前面（原码表示）
    - 具体的编码方式有原码、补码、反码、移码
    - 每种编码方式都分为定点纯整数和定点纯小数的编码
- 浮点数：一定有符号

原码、补码、反码、移码详细定义 + 原码 * 纯整数：最高位是符号位，0为正，1为负，其余位为绝对值 * 纯小数：最高位即小数点左1位是符号位，其余位为绝对值 + 补码 * 纯整数：正数表示同原码，负数表示为其绝对值原码的取反加1。补码的符号位可以看作位权是，这里n表示非符号的数字位数 * 纯小数：正数表示同原码，负数表示为其绝对值原码的取反加1（加到最右边的小数位） + 反码 * 纯整数：正数表示同原码，负数表示位其绝对值原码的取反 * 纯小数：正数表示同原码，负数表示位其绝对值原码的取反 + 移码 * n位移码是在真值上加一个偏置 * 0的移码是，共个 * 真值的移码和补码仅符号位不同

运算方法和运算电路

运算器

运算器组成
- ALU：核心部件，完成各种算术和逻辑运算
- ACC：常用部件，可以提供源操作数，同时作为运算结果的目的操作数存放地
- PSW：重要部件，存放状态标志位，包括
  - CF：进位或借位标志，无符号数运算是否超过范围
  - OF：溢出标志，带符号数运算是否超过范围
  - SF：符号标志，负为1，非负为0
  - ZF：零标志，运算结果是否为零
  - PF：奇偶标志，运算结果低8位中1的个数是否位偶数，是则1，否则0
- 通用寄存器组：必要部件，用户编程可用，暂存参与运算的操作数和结果，存取快，数量少
- 专用/特殊寄存器组：用户编程不可使用，运算器内部寄存器
运算器结构
- 单总线结构：1条总线，3个周期（存源操作数1、存源操作数2、存计算结果），操作慢，电路简单
- 双总线结构：2条总线，2个周期（存源操作数1和源操作数2、存计算结果），操作较快，电路较复杂
- 三总线结构：3条总线，1个周期（存源操作数1和源操作数2并计算结果），操作快，电路复杂

基本运算部件

加法器

不带标志位的加法器，只能无符号数使用

一位全加器
- 输入，输出
串行加法器
- 只有一个全加器，数据逐行串行送入加法器
- n位操作数要进行n次操作，每次产生1位和
- 成本低，运算慢
并行加法器
- 由多个加法器组成，位数和机器字长相同，并行运算
- 运算时间主要是由进位的传递时间决定，加法器本身是次要因素
- 记为进位产生函数
- 记为进位传递函数
- 串行进位（波进位）：n个全加器串接，低位进位产生时间影响高位运算，位数越多延迟越多
- 并行进位（先行进位）：把高位进位在表达式上转化成最低位进位
  - 以此类推
  - 这种进位和字长无关，是快速的
  - 但位数太多时电路非常复杂
- 分组并行进位：把n位全加器分成若干组，组内并行进位，组间串或并行进位
  - 单级先行进位：组内并行（例如4位先行进位电路CLA），组间串行
  - 多级先行进位：组内并行（例如组内修改成4位成组先行进位电路BCLA），组间并行（CLA）

算术逻辑部件

带标志加法器
- 溢出标志，标志供有符号数使用
- 符号标志：和的符号
- 零标志：和为0
- 进位/借位标志，前者即，后者加法为0，减法为1，标志供无符号数使用
算术逻辑单元ALU
- 能实现多种算术运算和逻辑运算
- 核心是带标志加法器
- 输入包括
  - $、$ 两个n位操作数，
  - 进位输入
  - ALUop操作控制输入
- 输出包括
  - 进位输出
  - 输出
  - 各种标志位

加减运算

补码加减运算器可以实现无符号数和带符号数的加减操作，原理如下

减法看作是加上相反数（以补码的规则按位取反加1）
在加法器基础上，增加一个2选1多路选择器，根据控制信号来选择加还是减
- 如果选加则直接输入，如果选减，则减数按位取反
控制信号作为输入加法器，表示减数加1
ZF零标志对于有符号无符号数都有意义
CF进/借位标志，等于，无符号数使用
OF溢出标志，有符号数使用，判定方法有
- 单符号判定法：输入两个正数输出负数，或输入两个负数输出正数
- 双符号判定法：两个符号位不一致则溢出，较高位为实际符号
- 进位判定法：符号位进位和最高数位进位相同则没有溢出（异或运算）

乘除运算

乘除运算基本原理

原码1位乘法
- 原理：符号位单独运算，数值部分进行类似于笔算的步骤，从被乘数的低位开始，反复做加法和右移
- 算法：设 $原原$
  - 符号位为，数值取绝对值进行计算
  - 部分积取双符号位，初值为0
  - 从乘数最低位开始判断：为1则部分积加，为0则部分积加0。
  - 部分积右移1位
  - 重复n次判断
- 分析：累加n次，移位n次
补码1位乘法（Booth算法）
- 原理：
  - 符号位参与运算
  - $补补补$
  - 即 $补补$
- 算法：设 $补补$
  - 符号位参与运算，数取补码表示
  - 部分积取双符号位，初值为0
  - 从乘数最低位的差值开始判断（这里是最低非0位后面的第一个0）：为1则加 $补$ ，为0则加0，为-1则加 $补$
  - 部分积右移1位
  - 重复n次判断（判断至）
  - 判断最后一次，为1则加 $补$ ，为0则加0，为-1则加 $补$
- 分析：累加n+1次，移位n次（因为最后一次不需要移位）
原码除法（恢复余数法）
- 原理：
  - 符号位单独运算
  - 数值部分进行类似于笔算的步骤，只考虑被除数和除数都非0的情况，从被除数的高位开始，反复做减法和左移，注意余数不够减时需要恢复到减之前的余数
- 算法：设 $原原$
  - 符号位为，数值取绝对值进行计算
  - 先用被除数减除数，得到余数
  - 余数为正，上商“1”，左移余数后减除数（即）
  - 余数为负，上商“0”，先恢复到减之前的余数，再左移余数后减除数（即）。
  - 商的小数点后面需要上n个数，若末位上1，即余数为正则算法结束；若末位上0，即余数为负，需要恢复到减之前的余数，即余数加上
- 分析：n+1次减法，每次减法都有可能需要恢复余数（0到n+1次加法），n次移位
原码除法（不恢复余数法/加减交替法）
- 原理：
  - 符号位单独运算
  - 数值部分计算几乎和恢复余数法相同，只是对余数恢复步骤进行了优化
- 算法：设 $原原$
  - 符号位为，数值取绝对值进行计算
  - 先用被除数减除数，得到余数
  - 余数为正，上商“1”，左移余数后减除数（即）
  - 余数为负，上商“0”，左移余数后加除数（即）。
  - 商的小数点后面需要上n个数，若末位上1，即余数为正则算法结束；若末位上0，即余数为负，需要恢复到减之前的余数，即余数加上
- 分析：n+1次减法，最后一次减法后可能需要恢复余数（0或1次加法），n次移位
补码除法（加减交替法）
- 原理：
  - 符号位参与运算
  - 被除数和除数都用补码表示，商和余数也用补码表示
  - 商用单符号，被除数、除数、余数都用双符号表示
- 算法：设 $补补$
  - 被除数和除数，如果同号则被除数减除数；如果异号则被除数加除数
  - 余数和除数，同号则商上“1”，余数左移1位再减除数；异号则商上“0”，余数左移1位再加除数
  - 重复上一步n次，再把末位置1
- 分析：n+1次减法，n次移位，商末位恒设置为1

注： + 从原理上，乘法把两个n位数变为2n位；除法用2n位数除以n位数得到n位数 + 前面的原理总结是关于纯小数的乘法和除法，而整数的乘法除法基本差不多步骤，需要注意的是被除数高位或低位补0使得变为2n位 + 记忆：乘法右移n次，除法左移n次，原码乘法加n次，补码乘法加n+1次（符号位参与运算，相邻位作差），原码恢复余数除法减2n+1到4n+2次，原码不恢复余数法减2n+1到2n+2次，补码加减交替除法减2n+1次（符号参与运算，同号上1减，异号上0加）

乘法电路和除法电路基本结构

32位无符号乘法运算电路基本结构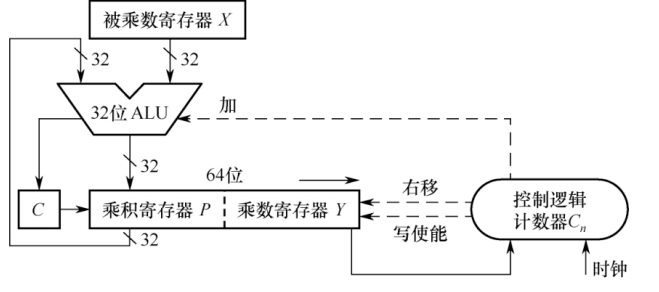

32位补码一位乘法运算电路基本结构（对应Booth算法）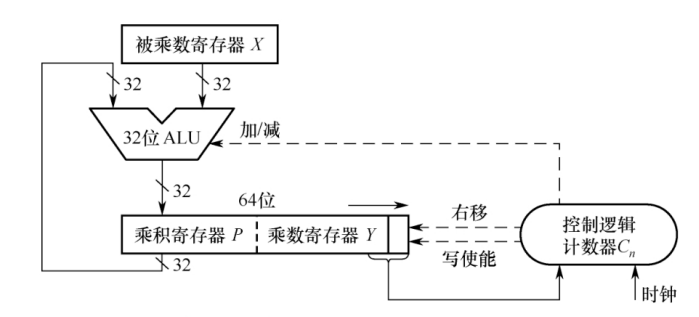

32位除法运算电路基本结构（对应原码的不恢复余数法/补码加减交替法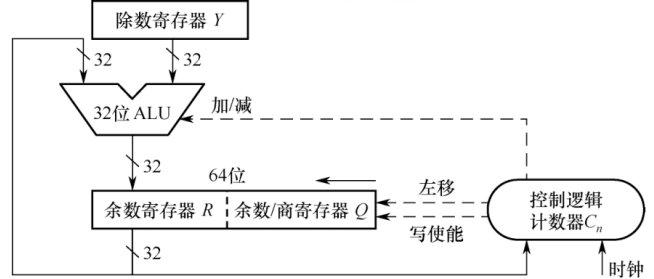）可以看出，如果该图的控制逻辑中考虑除数的符号，则对应补码的加减交替法

移位运算

逻辑移位
- 操作数视为无符号数
- 不丢失有效数值位的情况下，左移等价于乘以2，右移等价于除以2
- 空位补0
算术移位
- 操作数视为有符号数
- 不丢失有效数值位的情况下，左移等价于乘以2，右移等价于除以2
- 由上一条易知，负数补码右移时空位补1，负数反码左移右移空位都补1，其他情况空位补0
循环移位
- 小循环左移：不带CF的循环左移，CF不参与循环，CF=MSB，LSB=MSB
- 小循环右移：不带CF的循环右移，CF不参与循环，CF=LSB，MSB=LSB
- 大循环左移：带CF的循环左移，CF参与循环，CF=MSB，LSB=CF
- 大循环右移：带CF的循环右移，CF参与循环，CF=LSB，MSB=CF

整数的表示和运算

无符号整数的表示和运算

直接表示为二进制串
无符号整数的加法、乘法、除法前面都提到过，基本和带符号正数的原码运算规则类似
无符号整数的移位对应逻辑移位

带符号整数的表示和运算

通常用补码表示
补码的加法、乘法、除法规则前面都提到过
带符号整数的移位相当于算术移位

整数的类型转换

带符号数和无符号数的转换：不改变机器码的二进制串，但是改变机器码的解释，因此真值改变
不同字长数的转换
- 大字节转小字节：直接截断
- 小字节转大字节：不改变机器码的解释，因此不希望真值改变，从而根据机器码类型补0或1

浮点数的表示和运算

浮点数的表示

浮点数表示为，其中底数r通常是2，E和M都是带符号定点数，前者是阶码，后者是尾数
阶码一般用移码或补码表示，尾数一般用原码或补码表示
规范化浮点数：尾数最高位是1
左规：尾数算术左移1位，阶码减1，可能需要多次
右规：运算溢出时（双符号位01或10），则尾数算术右移1位，阶码加1，只需要一次
浮点数范围：从小到大分别为，负上溢、负数范围、负下溢、0、正下溢、正数范围、正上溢
规格化后的运算结果超过浮点数范围则为溢出，浮点数下溢时计算机通常当0处理
IEEE754标准
- 单精度浮点数float（1位符号S、8位阶码E、23位尾数M、共32位）表示为，符号S取0或1，阶码E取1-254
- 双精度浮点数double（1位符号S，11位阶码E，52位尾数M，共64位）表示为，符号S取0或1，阶码E取1-2046
- 阶码的移码偏置是127/1023，因为可以空出全1表示无穷大
- 尾数含有隐藏的1在小数点前面，尾数只保存小数点后面的值
- 0用全0表示，根据符号位可以分为+0和-0
- 无法规范化的数称为非规范化数，即阶码全0。此时偏置为126或1022，即阶码0和1对应值相等，同时非规范化数的尾数不包含隐藏的1，这样设置阶码和尾数的目的是为了平滑的从规范化数过渡到非规范化数
- 非规范化数提供了一种表示0的方式，但0不是非规范化数，最小的非规范化数是非0的
- 阶码全1，尾数全0，表示无穷大，根据符号位分为正无穷负无穷
- 阶码全1，尾数非全0，表示NaN（Not a Number），即用于无意义的数或在初始化时使用。
同样数值位长度的浮点数和定点数相比，表示范围增大，但精度降低

浮点数加减运算

对阶：小阶向大阶对齐，即阶码小的尾数（算术）右移阶加1，直到两个数阶码相等。右移时舍掉有效位会影响精度。计算时可以先算阶码的差
尾数求和：对阶后的尾数按定点数补码加减运算处理，带上双符号位，减法等于加补码对应的负数
规格化:左规或右规至补码最高数值位和符号位不同
舍入：右规造成的低位丢失，可以0舍1入，也可以末尾恒置1。前者的“1入”情况如果造成上溢，需要再右规一次，后者根据末尾原先的情况，可能造成结果变大或变小
溢出判断和处理：规格化尾数后，根据阶码是否超过范围来判断溢出情况，即补码表示的双符号位不一致（10下溢，01上溢）。

浮点数类型转换

int转float，不会溢出；可能有数据舍入从而丢失精度
int或float转double，不会溢出；且保持精度
double转float，可能溢出；可能有数据舍入从而丢失精度
double或float转int，可能溢出；可能有数据截断从而丢失精度
以上类型转换尽量保持真值不变，但由于编码方式不同，因此存储的二进制串会有改变
溢出主要看编码的表示范围
精度主要看编码的有效位数和表示范围的相对关系
- 同样的有效位数，表示范围约大，精度越低，比如float和int都是32个有效位，float范围大，精度低
- 同样的表示范围，编码有效位数越多，精度越高
- 注意到double相比float和int，即使表示范围更大，但因为有效位数更大，精度更大

数据的存储和排列

大端方式和小端方式

用最低有效字节LSB和最高有效字节MSB表示数的最高位和最低位
大端方式：按MSB到LSB的顺序存储数据
小端方式：按LSB到MSB的顺序存储数据
注意：一个地址内（一个字节）的数据无论按大端或小端存储，其机器级代码的文本形式中都是以实际值方式呈现

边界对齐

以32位存储字长的机器为例
字节：8位二进制长度，每个地址对应存储单元的大小
半字：半个存储字长，对应16位、2字节
字：存储字长，对应32位、4字节
边界对齐方式
- 半字地址一定是2的整数倍，字地址一定是4的整数倍
- 数据无论是字节、半字、字都可以一次取出
- 不满足上述条件可以通过填充0满足条件，浪费空间但提高取指令和取数的速度
非边界对齐方式
- 充分利用存储空间
- 半字长和字长的数据可能在两个存储字中，需要两次访存，还要对高低字节进行位置调整和连接，影响指令执行效率