【习题解答】线性时间选择

注： 本题解为个人完成，难免有疏漏，请勿抄袭，仅供参考，同时欢迎留言指正。 ## 5.2 假设5个数分别为。找中位数就是找第3小的数。

，若则，使得
，若则，使得
，若则，使得，且不影响，此时比至少3个数小，故不可能是第3小的数，于是接下来考虑中第2小的数
，若则，使得
，若则，使得，且不影响。故此时是四个数中的最小值，不可能是第2小；又比都大，故也不可能是第2小。故接下来考虑中较小的那个即可
，较小的那个是中位数

如果用决策树表示这个算法，每个非叶节点给出哪两个数之间比较，两个不同的比较结果分别导向左右子树。

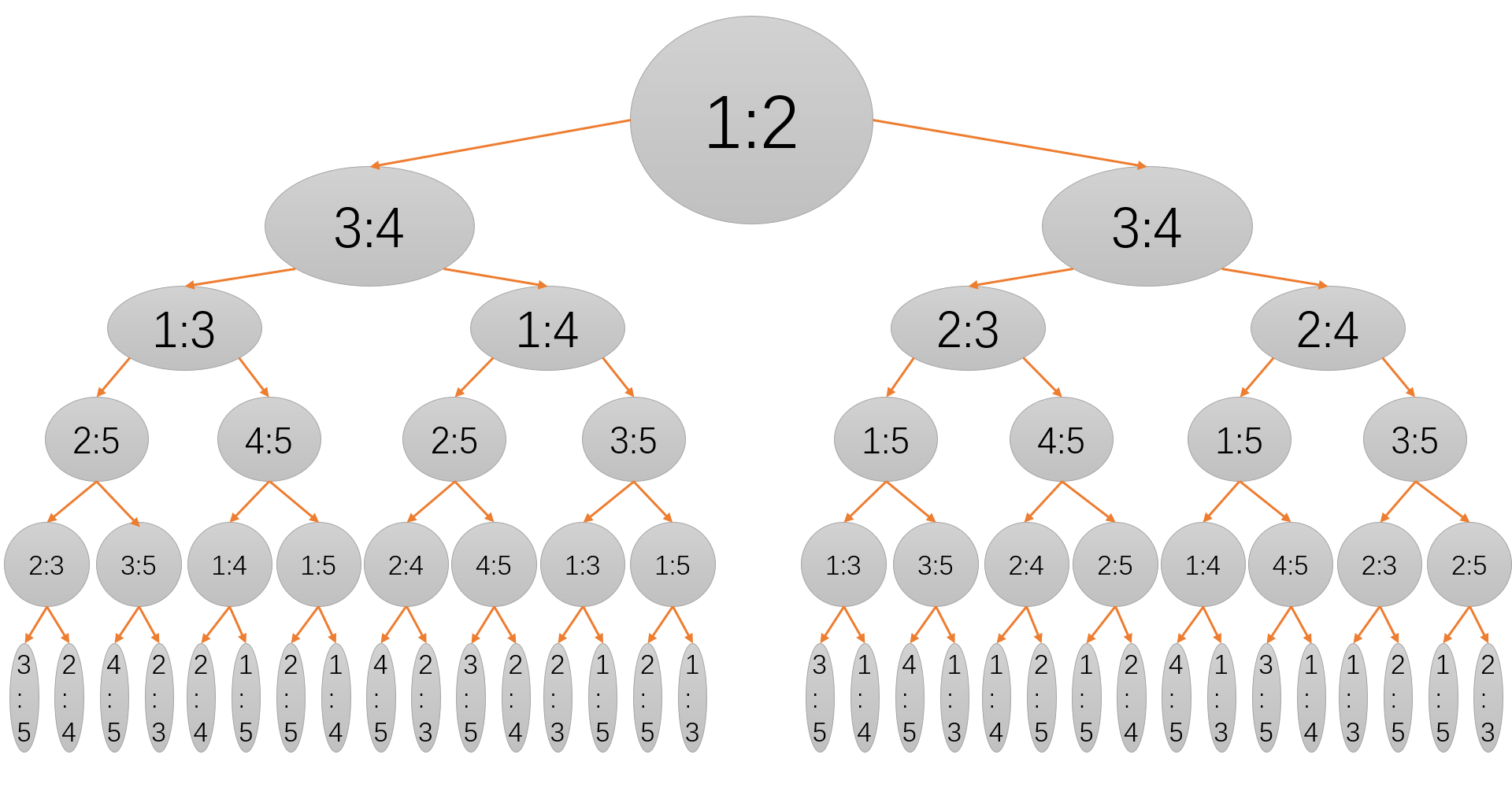
最后一层比较得到的较小者就是中位数，由于画的太密集，叶子节点没有画出来。

5.4

基于比较的算法来找阶为的数，我们可以用图的角度理解： + 个元素对应个点 + 给定一个比较，确定一个有向边，那么边的方向是从大元素到小元素的 + 那么算法结束时，找到了阶为的数，同时也构造了一个图 + 对于节点在中可以到达的所有节点的集合记为，所有可以到达节点的集合记为，其他的节点集合记为。

接下来以问答的形式进行深入思考： + 一定满足什么条件？ + 中的元素可以存在哪些边？ + 如果把中的每个节点都添加一条指向节点的边，会不会违背刚刚的条件？为什么？ + 的大小和的关系？ + 的大小和的关系？

想通上面的过程，原命题显然得证。

5.5

经典找中位数后二分，每次规模减半。

由主定理最坏情况复杂度还是

5.6

(1)

全部元素排序即可，如堆排、归并排序等，注意快排不行。

(2)

由自然想到用堆。

建堆，次pop是

(3)

由自然想到对前大的数进行冒泡排序(或选择排序)。

找第大数，并以此找到未排序的前大数

对个数冒泡排序。

(4)

由自然想到对前大的数进行堆排序。

找第大数，并以此找到未排序的前大数

对个数堆排序。

5.7

(1)

对n个数进行排序，
k次循环，每次选取中位数前后数中较近的那个数，

(2)

先找到中位数、以及第大的数、第大的数，
找到比中位数小，且最接近中位数的k个数，并排序，
找到比中位数大，且最接近中位数的k个数，并排序，
k次循环，每次选取中位数前后数中较近的那个数，

5.9

(1)

先找到A,B数组各自的第小的数a和b
若a小于b，则a的阶比k小，删除A的前个元素，反之删除B的前个元素
令
重复直至，思考为什么一定会到1？
A,B表头中较小的那个就是结果

复杂度是

(2)

先找到A,B数组各自的第小的数a,b,c
找到a,b,c中最小者，比如是a，则a的阶比k小，删除A的前个元素，反之删除B或C的前个元素
令
重复直至，思考为什么一定会落到这个范围？
重复取A,B,C表头中最小值次，注意此时

复杂度是

(3)

注：根据评论区的留言，更新了复杂度的计算过程，算出了复杂度更紧的上界

还是按照之前的思路即可: + 先找到每一行数组各自的第小的数 + 找到其中的最小者，比如是，则的阶比k小，删除第一行的前个元素，反之删除对应行的前个元素 + 令 + 重复直至，思考为什么一定会落到这个范围？ + 重复取m行表头中最小值次，且，这里带来的开销是，可以用堆优化为

我们分析一下总的复杂度：

每次几乎是变成原本的，因为base case是，则可以解停止条件，得比较次数，即比较次数大于，比如取即可达到base case。

注意:这里之所以说几乎，是因为有取整操作，即，但是这不影响的更新次数的量级，为什么？

可以这样想： + 对于的第次迭代，，考虑取整()和不取整()两个情况中的大小关系？的大小关系？ + 在不考虑取整时，之前分析过，最多迭代次，就会达到停止条件(即) + 那么考虑取整时，迭代次后，因为这个过程中存在取整的操作，此时可能还没达到停止条件(即)，但此时必然有，想一想为什么？故最多再迭代次就可以达到停止条件，想一想为什么？ + 因此，迭代次数的量级不受取整的影响，考虑取整时的迭代次数最多是没考虑取整时的迭代次数的两倍

继续分析原问题的复杂度，结合每次都要找m个数中的最小值，即O(m)，得到总的复杂度是

其中可以用泰勒展开改写成的形式，因此复杂度是

5.10

(1)

按定义证明即可

设中位数为，则其满足且

再证明此数满足加权中位数定义即可：且

(2)

使用最坏情况复杂度是的排序
遍历一遍，计算权重和，当不满足时停止，此时的即加权中位数
最好再证明一下正确性(是否满足定义的那两条)

(3)

线性时间选择找到中位数
若，对左半部分递归
若，对右半部分递归
否则就是加权中位数
有一个实现上的细节：应该维护两个全局变量，分别保存子区间外以左和以右的权重和，每次调用递归前更新，这样做的目的是每次计算权重和的只需要考虑子区间的范围，避免冗余的计算
用主定理分析复杂度为什么是